The Shape of Molecules

The Shape of Molecules

    The three dimensional shape or configuration of a molecule is an important characteristic. This shape is dependent on the preferred spatial orientation of covalent bonds to atoms having two or more bonding partners. Three dimensional configurations are best viewed with the aid of models. 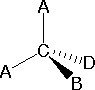In order to represent such configurations on a two-dimensional surface (paper, blackboard or screen), we often use perspective drawings in which the direction of a bond is specified by the line connecting the bonded atoms.In most cases the focus of configuration is a carbon atom so the lines specifying bond directions will originate there. As defined in the diagram on the right, a simple straight line represents a bond lying approximately in the surface plane. The two bonds to substituents A in the structure on the left are of this kind. A wedge shaped bond is directed in front of this plane (thick end toward the viewer), as shown by the bond to substituent B; and a hatched bond is directed in back of the plane (away from the viewer), as shown by the bond to substituent D. Some texts and other sources may use a dashed bond in the same manner as we have defined the hatched bond, but this can be confusing because the dashed bond is often used to represent a partial bond (i.e. a covalent bond that is partially formed or partially broken). The following examples make use of this notation, and also illustrate the importance of including non-bonding valence shell electron pairs (colored blue) when viewing such configurations .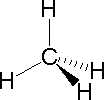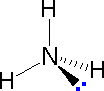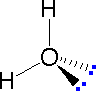

Methane		Ammonia		Water

Bonding configurations are readily predicted by valence-shell electron-pair repulsion theory, commonly referred to as VSEPR in most introductory chemistry texts. This simple model is based on the fact that electrons repel each other, and that it is reasonable to expect that the bonds and non-bonding valence electron pairs associated with a given atom will prefer to be as far apart as possible. The bonding configurations of carbon are easy to remember, since there are only three categories.

Configuration	Bonding Partners	Bond Angles	Example
Tetrahedral	4	109.5º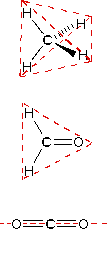
Trigonal	3	120º
Linear	2	180º

In the three examples shown above, the central atom (carbon) does not have any non-bonding valence electrons; consequently the configuration may be estimated from the number of bonding partners alone. For molecules of water and ammonia, however, the non-bonding electrons must be included in the calculation. In each case there are four regions of electron density associated with the valence shell so that a tetrahedral bond angle is expected. The measured bond angles of these compounds (H₂O 104.5º & NH₃ 107.3º) show that they are closer to being tetrahedral than trigonal or linear. Of course, it is the configuration of atoms (not electrons) that defines the the shape of a molecule, and in this sense ammonia is said to be pyramidal (not tetrahedral). The compound boron trifluoride, BF₃, does not have non-bonding valence electrons and the configuration of its atoms is trigonal. 

The best way to study the three-dimensional shapes of molecules is by using molecular models. Many kinds of model kits are available to students and professional chemists. Some of the useful features of physical models can be approximated by the model viewing applet Jmol. This powerful visualization tool allows the user to move a molecular stucture in any way desired. Atom distances and angles are easily determined. To measure a distance, double-click on two atoms. To measure a bond angle, do a double-click, single-click, double-click on three atoms. To measure a torsion angle, do a double-click, single-click, single-click, double-click on four atoms. A pop-up menu of commands may be accessed by the right button on a PC or a control-click on a Mac while the cursor is inside the display frame.

One way in which the shapes of molecules manifest themselves experimentally is through molecular dipole moments. A molecule which has one or more polar covalent bonds may have a dipole moment as a result of the accumulated bond dipoles. In the case of water, we know that the O-H covalent bond is polar, due to the different electronegativities of hydrogen and oxygen. Since there are two O-H bonds in water, their bond dipoles will interact and may result in a molecular dipole which can be measured. The following diagram shows four possible orientations of the O-H bonds.

The bond dipoles are colored magenta and the resulting molecular dipole is colored blue. In the linear configuration (bond angle 180º) the bond dipoles cancel, and the molecular dipole is zero. For other bond angles (120 to 90º) the molecular dipole would vary in size, being largest for the 90º configuration. In a similar manner the configurations of methane (CH₄) and carbon dioxide (CO₂) may be deduced from their zero molecular dipole moments. Since the bond dipoles have canceled, the configurations of these molecules must be tetrahedral (or square-planar) and linear respectively.
The case of methane provides insight to other arguments that have been used to confirm its tetrahedral configuration. For purposes of discussion we shall consider three other configurations for CH₄, square-planar, square-pyramidal and triangular-pyramidal. 

Substitution of one hydrogen by a chlorine atom gives a CH₃Cl compound. Since the tetrahedral, square-planar and square-pyramidal configurations have structurally equivalent hydrogen atoms, they would each give a single substitution product. However, in the trigonal-pyramidal configuration one hydrogen (the apex) is structurally different from the other three (the pyramid base). Substitution in this case should give two different CH₃Cl compounds if all the hydrogens react. In the case of disubstitution, the tetrahedral configuration of methane would lead to a single CH₂Cl₂ product, but the other configurations would give two different CH₂Cl₂ compounds. These substitution possibilities are shown in the above insert.

Hybridization of Nitrogen, Oxygen, Phosphorus, and Sulfur

In addition to forming single and double bonds by sharing two and four elec- trons, respectively, carbon also can form a triple bond by sharing six electrons. To account for the triple bond in a molecule such as acetylene, H O C q C O H, we need a third kind of hybrid orbital, an sp hybrid. Imagine that, instead of combining with two or three p orbitals, a carbon 2s orbital hybridizes with only a single p orbital. Two sp hybrid orbitals result, and two p orbitals remain unchanged. The two sp orbitals are oriented 180° apart on the x-axis, while the remaining two p orbitals are perpendicular on the y-axis and the z-axis.

When two sp carbon atoms approach each other, sp hybrid orbitals on each carbon overlap head-on to form a strong sp–sp s bond. At the same time, the pz orbitals from each carbon form a pz–pz p bond by sideways overlap, and the py orbitals overlap similarly to form a py–py p bond. The net effect is the sharing of six electrons and formation of a carbon–carbon triple bond. The two remain- ing sp hybrid orbitals each form a s bond with hydrogen to complete the acety- lene molecule.

As suggested by sp hybridization, acetylene is a linear molecule with H]C]C bond angles of 180°. The C]H bonds have a length of 106 pm and a strength of 558 kJ/mol (133 kcal/mol). The C-C bond length in acetylene is 120 pm, and its strength is about 965 kJ/mol (231 kcal/mol), making it the shortest and strongest of any carbon–carbon bond.

sp2 Hybrid Orbitals and the Structure of Ethylene

The same kind of orbital hybridization that accounts for the methane structure also accounts for the bonding together of carbon atoms into chains and rings to make possible many millions of organic compounds. Ethane, C2H6, is the simplest molecule containing a carbon–carbon bond.

We can picture the ethane molecule by imagining that the two carbon atoms bond to each other by s overlap of an sp3 hybrid orbital from each. The remaining three sp3 hybrid orbitals on each carbon over- lap with the 1s orbitals of three hydrogens to form the six C]H bonds. The C]H bonds in ethane are similar to those in methane, although a bit weaker—421 kJ/mol (101 kcal/mol) for ethane versus 439 kJ/mol for methane. The C ] C bond is 154 pm long and has a strength of 377 kJ/mol (90 kcal/mol). All the bond angles of ethane are near, although not exactly at, the tetra- hedral value of 109.5°.

sp3 Hybrid Orbitals and the Structure of Methane

The bonding in the hydrogen molecule is fairly straightforward, but the situ- ation is more complicated in organic molecules with tetravalent carbon atoms. Take methane, CH4, for instance. As we’ve seen, carbon has four valence electrons (2s2 2p2) and forms four bonds. Because carbon uses two kinds of orbitals for bonding, 2s and 2p, we might expect methane to have two kinds of C ] H bonds. In fact, though, all four C ] H bonds in methane are identical and are spatially oriented toward the corners of a regular tetrahedron. How can we explain this?

An answer was provided in 1931 by Linus Pauling, who showed mathemat- ically how an s orbital and three p orbitals on an atom can combine, or hybrid- ize, to form four equivalent atomic orbitals with tetrahedral orientation. These tetrahedrally oriented orbitals are called sp3 hybrids. Note that the superscript 3 in the name sp3 tells how many of each type of atomic orbital combine to form the hybrid, not how many elec- trons occupy it.

The concept of hybridization explains how carbon forms four equivalent tetrahedral bonds but not why it does so. The shape of the hybrid orbital suggests the answer. When an s orbital hybridizes with three p orbitals, the resultant sp3 hybrid orbitals are unsymmetrical about the nucleus. One of the two lobes is larger than the other and can therefore overlap more effec- tively with an orbital from another atom to form a bond. As a result, sp3 hybrid orbitals form stronger bonds than do unhybridized s or p orbitals.

The asymmetry of sp3 orbitals arises because, as noted previously, the two lobes of a p orbital have different algebraic signs, 1 and 2, in the wave func- tion. Thus, when a p orbital hybridizes with an s orbital, the positive p lobe adds to the s orbital but the negative p lobe subtracts from the s orbital. The resultant hybrid orbital is therefore unsymmetrical about the nucleus and is strongly oriented in one direction.

When each of the four identical sp3 hybrid orbitals of a carbon atom overlaps with the 1s orbital of a hydrogen atom, four identical C]H bonds are formed and methane results. Each C ] H bond in methane has a strength of 439 kJ/mol (105 kcal/mol) and a length of 109 pm. Because the four bonds have a specific geometry, we also can define a property called the bond angle. The angle formed by each H ] C ] H is 109.5°, the so-called tetrahedral angle. 

Describing Chemical Bonds: Valence Bond Theory

How does electron sharing lead to bonding between atoms? Two models have been developed to describe covalent bonding: valence bond theory and molecular orbital theory. Each model has its strengths and weaknesses, and chemists tend to use them interchangeably depending on the circumstances. Valence bond theory is the more easily visualized of the two, so most of the descriptions we’ll use in this book derive from that approach.

According to valence bond theory, a covalent bond forms when two atoms approach each other closely and a singly occupied orbital on one atom overlaps a singly occupied orbital on the other atom. The electrons are now paired in the overlapping orbitals and are attracted to the nuclei of both atoms, thus bond- ing the atoms together. In the H2 molecule, for instance, the H ] H bond results from the overlap of two singly occupied hydrogen 1s orbitals.

The overlapping orbitals in the H2 molecule have the elongated egg shape we might get by pressing two spheres together. If a plane were to pass through the middle of the bond, the intersection of the plane and the overlapping orbit- als would be a circle. In other words, the H]H bond is cylindrically symmetri- cal. Such bonds, which are formed by the head-on overlap of two atomic orbitals along a line drawn between the nuclei, are called sigma (s) bonds.

During the bond-forming reaction 2 H∙ n H2, 436 kJ/mol (104 kcal/mol) of energy is released. Because the product H2 molecule has 436 kJ/mol less energy than the starting 2 H∙ atoms, the product is more stable than the reactant and we say that the H ] H bond has a bond strength of 436 kJ/mol. In other words, we would have to put 436 kJ/mol of energy into the H]H bond to break the H2 molecule apart into H atoms. [For convenience, we’ll generally give energies in both kilocalories (kcal) and the SI unit kilojoules (kJ): 1 kJ 5 0.2390 kcal; 1 kcal 5 4.184 kJ.]

How close are the two nuclei in the H2 molecule? If they are too close, they will repel each other because both are positively charged, yet if they’re too far apart, they won’t be able to share the bonding electrons. Thus, there is an opti- mum distance between nuclei that leads to maximum stability. Called the bond length, this distance is 74 pm in the H2 molecule. Every cova- lent bond has both a characteristic bond strength and bond length.

Development of Chemical Bonding Theory

By the mid-1800s, the new science of chemistry was developing rapidly and chemists had begun to probe the forces holding compounds together. In 1858, August Kekulé and Archibald Couper independently proposed that, in all organic compounds, carbon is tetravalent—it always forms four bonds when it joins other elements to form stable compounds. Furthermore, said Kekulé, car- bon atoms can bond to one another to form extended chains of linked atoms. In 1865, Kekulé provided another major advance when he suggested that carbon chains can double back on themselves to form rings of atoms.

Although Kekulé and Couper were correct in describing the tetravalent nature of carbon, chemistry was still viewed in a two-dimensional way until 1874. In that year, Jacobus van’t Hoff and Joseph Le Bel added a third dimen- sion to our ideas about organic compounds when they proposed that the four bonds of carbon are not oriented randomly but have specific spatial directions. Van’t Hoff went even further and suggested that the four atoms to which car- bon is bonded sit at the corners of a regular tetrahedron, with carbon in the center.

Note the conventions used to show three-dimensionality: solid lines represent bonds in the plane of the page, the heavy wedged line represents a bond coming out of the page toward the viewer, and the dashed line represents a bond receding back behind the page, away from the viewer. These representations will be used throughout the text.

Why, though, do atoms bond together, and how can bonds be described electronically? The why question is relatively easy to answer: atoms bond together because the compound that results is more stable and lower in energy than the separate atoms. Energy—usually as heat—always flows out of the chemical system when a bond forms. Conversely, energy must be put into the chemical system to break a bond. Making bonds always releases energy, and breaking bonds always absorbs energy. The how question is more difficult. To answer it, we need to know more about the electronic properties of atoms.

We know through observation that eight electrons (an electron octet) in an atom’s outermost shell, or valence shell, impart special stability to the noble- gas elements in group 8A of the periodic table: Ne (2 , 8); Ar (2 , 8 , 8); Kr (2 , 8 , 18, 8). We also know that the chemistry of main-group elements is governed by their tendency to take on the electron configuration of the nearestnoble gas. The alkali metals in group 1A, for example, achieve a noble-gas con- figuration by losing the single s electron from their valence shell to form a cation, while the halogens in group 7A achieve a noble-gas configuration by gaining a p electron to fill their valence shell and form an anion. The resultant ions are held together in compounds like Na1 Cl2 by an electrostatic attraction that we call an ionic bond.

But how do elements closer to the middle of the periodic table form bonds? Look at methane, CH4, the main constituent of natural gas, for example. The bonding in methane is not ionic because it would take too much energy for carbon (1s2 2s2 2p2) either to gain or lose four electrons to achieve a noble-gas configuration. As a result, carbon bonds to other atoms, not by gaining or losing electrons, but by sharing them. Such a shared-electron bond, first pro- posed in 1916 by G. N. Lewis, is called a covalent bond. The neutral collection of atoms held together by covalent bonds is called a molecule.

A simple way of indicating the covalent bonds in molecules is to use what are called Lewis structures, or electron-dot structures, in which the valence- shell electrons of an atom are represented as dots. Thus, hydrogen has one dot representing its 1s electron, carbon has four dots (2s2 2p2), oxygen has six dots (2s2 2p4), and so on. A stable molecule results whenever a noble-gas configura- tion is achieved for all the atoms—eight dots (an octet) for main-group atoms or two dots for hydrogen. Simpler still is the use of Kekulé structures, or line- bond structures, in which a two-electron covalent bond is indicated as a line drawn between atoms.

The number of covalent bonds an atom forms depends on how many addi- tional valence electrons it needs to reach a noble-gas configuration. Hydrogen has one valence electron (1s) and needs one more to reach the helium configu- ration (1s2), so it forms one bond. Carbon has four valence electrons (2s2 2p2) and needs four more to reach the neon configuration (2s2 2p6), so it forms four bonds. Nitrogen has five valence electrons (2s2 2p3), needs three more, and forms three bonds; oxygen has six valence electrons (2s2 2p4), needs two more, and forms two bonds; and the halogens have seven valence electrons, need one more, and form one bond.

Valence electrons that are not used for bonding are called lone-pair electrons, or nonbonding electrons. The nitrogen atom in ammonia, NH3, for instance, shares six valence electrons in three covalent bonds and has its remaining two valence electrons in a nonbonding lone pair. As a time-saving shorthand, nonbonding electrons are often omitted when drawing line-bond structures, but you still have to keep them in mind since they’re often crucial in chemical reactions.

Atomic Structure: Electron Configurations

The lowest-energy arrangement, or ground-state electron configuration, of an atom is a listing of the orbitals occupied by its electrons. We can predict this arrangement by following three rules.

Rule 1

The lowest-energy orbitals fill up first, according to the order 1s n 2s n 2p n 3s n 3p n 4s n 3d, a statement called the aufbau principle. Note that the 4s orbital lies between the 3p and 3d orbitals in energy.

Rule 2

Electrons act in some ways as if they were spinning around an axis, some- what as the earth spins. This spin can have two orientations, denoted as up (h) and down (g). Only two electrons can occupy an orbital, and they must be of opposite spin, a statement called the Pauli exclusion principle.

Rule 3

If two or more empty orbitals of equal energy are available, one electron occupies each with spins parallel until all orbitals are half-full, a statement called Hund’s rule.

Hydrogen, for instance, has only one electron, which must occupy the lowest-energy orbital. Thus, hydrogen has a 1s ground-state configuration. Carbon has six electrons and the ground-state configuration 1s2 2s2 2px1 2py1, and so forth. Note that a superscript is used to represent the number of electrons in a particu- lar orbital.

AtomicStructure:Orbitals

How are the electrons distributed in an atom? You might recall from your gen- eral chemistry course that, according to the quantum mechanical model, the behavior of a specific electron in an atom can be described by a mathematical expression called a wave equation—the same type of expression used to describe the motion of waves in a fluid. The solution to a wave equation is called a wave function, or orbital, and is denoted by the Greek letter psi (c).

By plotting the square of the wave function, c2, in three-dimensional space, an orbital describes the volume of space around a nucleus that an electron is most likely to occupy. You might therefore think of an orbital as looking like a photograph of the electron taken at a slow shutter speed. In such a photo, the orbital would appear as a blurry cloud, indicating the region of space where the electron has been. This electron cloud doesn’t have a sharp bound- ary, but for practical purposes we can set the limits by saying that an orbital represents the space where an electron spends 90% to 95% of its time.

What do orbitals look like? There are four different kinds of orbitals, denoted s, p, d, and f, each with a different shape. Of the four, we’ll be concerned primar- ily with s and p orbitals because these are the most common in organic and biological chemistry. An s orbital is spherical, with the nucleus at its center; a p orbital is dumbbell-shaped; and four of the five d orbitals are cloverleaf- shaped. The fifth d orbital is shaped like an elongated dumbbell with a doughnut around its middle.

The orbitals in an atom are organized into different electron shells, centered around the nucleus and having successively larger size and energy. Different shells contain different numbers and kinds of orbitals, and each orbital within a shell can be occupied by two electrons. The first shell contains only a single s orbital, denoted 1s, and thus holds only 2 electrons. The second shell contains one 2s orbital and three 2p orbitals and thus holds a total of 8 electrons. The third shell contains a 3s orbital, three 3p orbitals, and five 3d orbitals, for a total capacity of 18 electrons. 

The three different p orbitals within a given shell are oriented in space along mutually perpendicular directions, denoted px, py, and pz.

Atomic Structure

Atomic Structure 

Elements are described by: 

Atomic number (Z): number of protons in the nucleus [same as the number of electrons]

Mass number (A): total of protons and neutrons in the nucleus!

Isotopes of an element have the same value of Z but different values of A.